
| Home |
|---|
| Staff |
| Events |
| Lehre/Teaching |
| PRisMa Lab |
| FAM goes public |
| Infobroschüre |
| Simulations |
| Posters |
| Press Articles |
| Jobs |
| Contact |
| FAM-ily (local) |
| |
Hedgen & Versichern
Worum geht es in der Finanz- und Versicherungsmathematik? Im folgenden versuchen wir beispielhaft, einen Eindruck von den wesentlichen Begriffen zu geben: ihrer wirtschaftlichen Bedeutung einerseits und ihrer mathematischen Modellierung andererseits.
Grob gesagt ist der Unterschied zwischen Finanzmathematik und Versicherungsmathematik derselbe wie zwischen „hedgen“ und „versichern“. Den neudeutschen Ausdruck hedgen könnte man mit absichern übersetzen. Er ist seit dem Wirtschaftsnobelpreis für Merton und Scholes 1997 für die Black-Scholes-Optionspreisformel in aller Munde. Was ist also der Unterschied zwischen ab- und versichern?
Betrachten wir das Beispiel eines Maschinenbauers, der mit einem amerikanischen Kunden einen Vertrag über die Lieferung einer Maschine abschließt.
| Vertragsabschluss: | heute |
| Lieferfrist: | 6 Monate |
| Zahlung nach Auslieferung in die USA: | 100 Mio $ |
Für den Maschinenbauer ist dieses Geschäft mit mehreren Risiken verbunden. Wir greifen hier zwei heraus.
Transportrisiko: Die Maschine könnte während des Transports nach Amerika teilweise oder sogar irreparabel beschädigt werden.
Währungsrisiko: In sechs Monaten könnte der Dollarkurs so weit fallen, dass das Geschäft für den Maschinenbauer nicht mehr rentabel ist. Für das Beispiel nehmen wir an, dass ein €-Preis von 60 Mio. € für die Maschine gerade noch kostendeckend wäre, d.h. ein Dollarkurs von 0,6 Euro pro Dollar wäre gerade noch erträglich, bei einem niedrigeren Dollarkurs würde das Unternehmen aber Verluste machen.

Gegen das Transportrisiko kann sich der Maschinenbauer bei einer Versicherungsgesellschaft versichern. Wie berechnet das Unternehmen die Prämie?
Versicherungsprämie
Das Versicherungsunternehmen wird versuchen, aufgrund von Statistiken über Transportschäden in der Vergangenheit den Erwartungswert der Schadenssumme zu schätzen, um daraus die Prämie kalkulieren zu können.
Der Erwartungswert ist die Mindestprämie, die das Unternehmen verlangen muss, wenn es im Mittel die eintretenden Schäden durch die Prämieneinnahmen abdecken will. Tatsächlich wird das Unternehmen zusätzlich zu der Mindestprämie noch einen Sicherheitszuschlag verlangen. Die Höhe dieses Zuschlages könnte zum Beispiel davon abhängen, ob im Mittel bei Transportschäden die Schadenssummen stark oder weniger stark vom Erwartungswert abweichen, d.h. wie groß die Standardabweichung der Schadenssumme ist.
Nehmen wir an, dass aus der Erfahrung bekannt ist, dass der mittlere prozentuale Schaden 0,2% und dass die Standardabweichung 0,1% beträgt. Damit ergibt sich für eine Versicherungssumme von 60 Mio. € eine Mindestprämie von 120.000 € und ein Sicherheitszuschlag in der Größenordnung von 60.000 €.
Das Versicherungsunternehmen bestimmt seine Prämie also auf der Grundlage eines statistischen Modells der Schadensverteilung und Schadenshäufigkeit. Das dafür nötige Know-how liefert die Versicherungsmathematik.
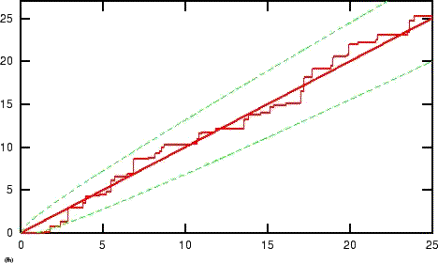
Gesamtschadensprozess eines Versicherungsportfolios:
Die Treppenfunktion beschreibt die aufaddierten Schäden, die Gerade stellt den mittleren Schadensverlauf dar, und die gestrichelten Linien geben die Standardabweichung vom Mittelwert an.
Optionspreis
Wie kann man sich gegen das Währungsrisiko schützen? Die Idee ist, ein Finanzgeschäft abzuschließen, das die möglichen Verluste begrenzt, aber leider auch die möglichen Gewinne schmälert. Um uns auf das Wesentliche beschränken zu können, betrachten wir das Beispiel stark vereinfacht.
Wir nehmen an, dass der Dollarkurs heute 0,7 €/$ beträgt und in sechs Monaten genau zwei Werte annehmen kann, nämlich 1,0 €/$ oder 0,5 €/$.
Das ist natürlich eher unrealistisch, weil prinzipiell jeder Wert möglich ist. In der Realität wären auch noch andere Aspekte zu beachten, wie etwa die (normalerweise unterschiedlichen) Zinsen in der Euro-Zone und den USA. Wir lassen dies alles jedoch außer Acht, um uns nicht in Details zu verlieren und die grundlegende Idee herausarbeiten zu können.
Wie bereits erwähnt, liegt die Verlustschwelle für den Maschinenbauer bei einem Wechselkurs von 0,6 € pro Dollar. Zur Absicherung könnte er deshalb heute sogenannte Put-Optionen mit Basispreis 0,6 € und Laufzeit sechs Monate kaufen. Diese Option gibt ihrem Käufer das Recht (aber nicht die Pflicht), nach sechs Monaten einen Dollar zum fixierten Wechselkurs von 0,6 €/$ an den Emittenten der Option zu verkaufen, auch wenn der Kurs am Fremdwährungsmarkt zwischenzeitlich unter 0,6 €/$ gefallen sein sollte. Wenn der Kurs nach sechs Monaten jedoch über 0,6 €/$ liegt, wird der Optionskäufer seine Dollar lieber auf dem freien Markt verkaufen und die Option verfallen lassen. Dem Emittenten der Option, d.h. dem Verkäufer der Option, entsteht im ungünstigen Fall ein Verlust (wenn der Kurs unter 0,6 €/$ fällt), und im günstigen Fall (Kurs über 0,6 €/$) erwachsen ihm in 6 Monaten keine Verpflichtungen aus dem Verkauf der Option. Es ist klar, dass er beim Verkauf der Option vom Käufer eine angemessene Entschädigung („fairer Preis“) erhalten muss.

Wechselkursentwicklung und Optionswert, heute und in 6 Monaten.
Was ist in diesem Fall angemessen? Naheliegend wäre, wie bei der Transportversicherung vorzugehen und den erwarteten Verlust des Optionsverkäufers zu bestimmen. Doch dazu müsste man insbesondere die Wahrscheinlichkeit kennen, dass der Kurs auf 0,5 €/$ fällt.
Überraschenderweise kann man jedoch bereits ohne Kenntnis der Wahrscheinlichkeiten für unser vereinfachtes Modell sagen, dass der faire Preis der Put-Option für einen Dollar mit Basispreis 0,6 € genau 0,06 € ist.
Wie kann man das begründen? Zunächst beobachten wir, dass in dem Fall, dass der Dollarkurs auf 0,5 €/$ fällt, der Optionskäufer die Option ausüben wird. Der Optionsverkäufer muss dann pro Optionsschein einen Dollar für 0,6 € vom Optionskäufer erwerben, erhält aber seinerseits beim Verkauf auf dem freien Markt nur 0,5 € pro Dollar. Im Ergebnis entspricht dies einer Zahlung von 0,1 € pro Optionsschein an den Optionskäufer.
Nehmen wir nun an, dass der Verkäufer vom Käufer 0,06 € für die Option auf einen Dollar erhält. Er kann sich dann pro Optionsschein noch 0,20 $ leihen und sofort zum aktuellen Kurs (0,7 € pro $) umtauschen und erhält dafür 0,14 €. Seine Vermögensbilanz unmittelbar nach dem Verkauf eines Optionsscheins lautet also: ein Guthaben von 0,20 € (0,14 € aus dem Umtausch plus 0,06 € aus dem Verkauf der Option) einerseits und Schulden von 0,20 $ andererseits.
Wie sieht die Situation nach Ablauf der 6 Monate aus? Fällt der Dollar in dieser Zeit auf 0,5 €/$, so kann der Optionsverkäufer seine $-Schuld von 0,20 $ für 0,10 € pro Optionsschein zurückzahlen und behält 0,1 € – genau soviel, wie er an den Optionskäufer zahlen muss. Steigt der Dollar auf 1,0 €/$, so kann der Optionsverkäufer exakt seine $-Schuld aus seinem €-Vermögen tilgen und macht weder Gewinn noch Verlust, hat aber andererseits auch keine Verpflichtungen gegenüber dem Optionskäufer.
Mittels der richtigen Dollarhandelsstrategie kann der Optionsverkäufer also exakt die Zahlungen reproduzieren, die er an den Optionskäufer zu leisten hat. Er braucht dazu ein Anfangsvermögen von 0,06 € – dies ist der faire Preis der Option. Ein höherer Preis ist nicht gerechtfertigt. Ein Preis von z.B. 0,07 € würde dazu führen, dass der Verkäufer die obige Strategie, für die er 0,06 € braucht, durchführt und 0,01 € risikolos verdienen würde. Dies nennt man Arbitragegewinn und dies wird in einer vernünftigen Optionspreistheorie ausgeschlossen. Ebensolchen risikolosen Gewinn kann man auch konstruieren, wenn der Preis kleiner als 0,06 € ist.
Wie oben erwähnt, ist dieses Modell viel zu simpel, um in dieser Form auf die Realität angewendet werden zu können. Es beinhaltet aber die entscheidende Idee. Um diese Idee auf realistische Modelle übertragen zu können – wie sie heute täglich von Investment-Banken und Broker-Häusern verwendet werden – bedarf es noch einiger spannender und interessanter Mathematik, für die wir hoffentlich Ihr Interesse geweckt haben.
[Bachelor- und Masterstudium Finanz- und Versicherungsmathematik]
(print version)
https://fam.tuwien.ac.at/public/hedging/index.php
Last modification: 2022-09-30
Imprint / Impressum — Privacy policy / Datenschutzerklärung